Puissance réactive : formule de calcul et unité VAR

Comment choisir sa puissance de compteur ?

L'offre du moment à -10,3 % (HT) par rapport au tarif réglementé
La puissance réactive, exprimée en kilovoltampère réactif (kVAR), est définie comme la part de l'électricité considérée comme étant "invisible" ou "inutile", car elle ne génère pas de travail thermique et n'est pas convertie directement en énergie utile sous forme de chaleur, de mouvement ou de lumière. La formule de calcul de la puissance réactive est : Q = S sin φ, où Q est la puissance réactive, S est la puissance apparente et sin φ le déphasage, en sachant que S = tension (U) x intensité (I).
- Tout savoir sur la puissance réactive
- La puissance réactive est exprimée en kilovoltampère réactif (kVAR).
- La puissance réactive est définie comme la part de l'électricité "non utile" ou invisible"
- La formule de calcul de la puissance réactive (Q) est :
- Q = S sin φ, où S = puissance apparente en kilovoltampère (kVA) et sin φ = déphasage en degré (º)
- S = UI, où U = tension en volt (V) et I = intensité en ampère (A)
C'est quoi la puissance réactive ?
La puissance réactive est considérée comme la partie "non utile" ou "invisible" de l'électricité, car elle n'est pas directement convertie en chaleur, mouvement ou lumière. Dans les installations électriques, seule une fraction de l'énergie est exploitée, tandis que le reste est perdu en raison des champs magnétiques produits par certains équipements électriques tels que les moteurs rotatifs, les appareils frigorifiques et les composants informatiques.
La puissance réactive se manifeste dans chaque système comportant des composants réactifs (qu'ils soient capacitifs ou inductifs). Elle peut être soit "générée" (dans un circuit capacitif) soit "consommée" (dans un circuit inductif) par les divers éléments des circuits.
Cette puissance réactive circule à travers le réseau électrique, entraînant un courant plus important et une surdimension des installations.
La puissance réactive parmi le triangle de puissance
Sur le marché de l'électricité, il existe trois types de puissances :
- la puissance active
- la puissance réactive
- la puissance apparente.
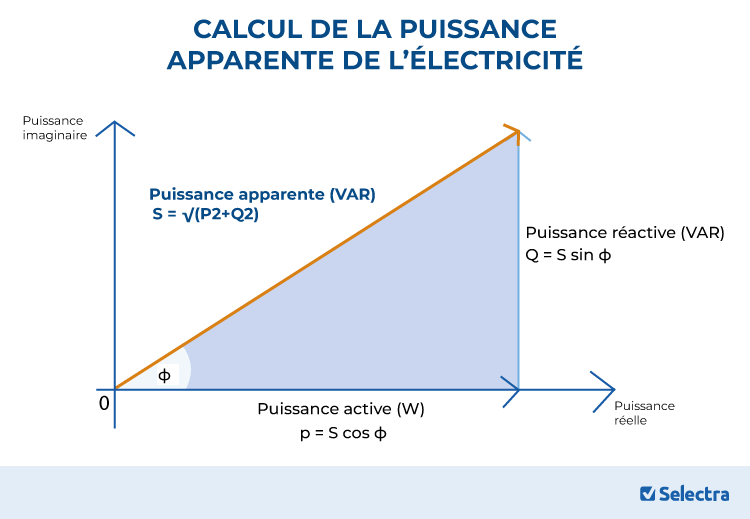
Ces puissances sont interdépendantes et sont représentées par le triangle des puissances.
Pour illustrer cela, on peut faire une analogie avec la mousse qui se forme au-dessus d'une bière. En utilisant les trois types de puissance, on peut dire que la puissance active représente la bière, la puissance réactive correspond à la mousse, et ensemble, elles forment la puissance apparente. Alors que la puissance active (la bière) est efficacement utilisée, la puissance réactive (la mousse) fait augmenter la puissance à transporter, tout comme la mousse augmente la quantité de bière dans le verre.
Quelle est unité de mesure pour la puissance réactive ?
Pour la puissance active consommée, on utilise le kilowatt (kW). La puissance réactive est exprimée en kilovoltampère réactif (kVAR). Quant à la puissance apparente, mesurée en kilovoltampère (kVA), elle dépend de la puissance active et réactive.
Cette somme dépend de l'angle formé entre la puissance apparente et la puissance active. Le cosinus et la tangente de cet angle déterminent l'importance de la partie réactive et permettent de calculer les surcharges.
Le rapport entre la puissance active et la puissance apparente est exprimé par le cosinus phi (cos φ) et la tangente phi (tan φ).
L'angle de déphasage ϕ correspond au décalage entre la tension (exprimée en volt) et l'intensité (exprimée en ampère) du courant électrique. Dans un système purement actif, il n'y a aucun déphasage entre ces deux grandeurs, et la puissance apparente est égale à la puissance active.
Lorsqu'un phénomène inductif se produit (comme en électromagnétisme), l'intensité "prend du retard" par rapport à la tension, ce qui crée un angle de déphasage.
En revanche, lorsque survient un phénomène capacitif (comme avec un condensateur), l'intensité "prend de l'avance" sur la tension, ce qui entraîne également un angle de déphasage.
Par conséquent, à un instant donné, il ne peut y avoir qu'une seule des deux puissances réactives, soit inductive, soit capacitive. Cependant, il est tout à fait possible de consommer les deux puissances réactives sur une durée de dix minutes. Par exemple, il est envisageable d'avoir un phénomène principalement inductif pendant cinq minutes, suivi d'un phénomène principalement capacitif pour les cinq minutes suivantes.
Mathématiquement, ces trois puissances sont représentées de la manière suivante :
Quelles sont les deux énergies de la puissance réactive ?
L'énergie réactive capacitive
L'énergie réactive capacitive est engendrée par des équipements électroniques tels que les condensateurs et les longs câbles. Il faut de l'énergie pour charger cette capacité.
L'énergie réactive inductive
L'énergie réactive inductive est principalement produite par des moteurs électriques et des transformateurs. Pour les charges inductives, une certaine quantité de puissance est requise pour magnétiser les bobines.
Quelle est la formule de calcul de la puissance réactive ?
La formule de calcul de la puissance réactive (VAR) est :
Q = S sin φ
Étant donné que S = UI, alors Q = UI sin φ
Où :
- Q = puissance réactive en voltampère réactif (VAR)
- S = puissance apparente en voltampère (VA)
- U = tension (V)
- I = intensité (A)
- sin φ = déphasage (º)
Exemple de la formule de calcul de la puissance réactive
Une lampe fluorescente fonctionnant à 220 volts (monophasé) en courant alternatif est alimentée. Un courant total de 0,3 ampère est enregistré. Cette lampe est composée d'un élément résistif, le tube lumineux, et d'un élément inductif, le ballast.
Le courant total présentera un déphasage de phi = 60°. Il se compose de la composante en phase avec la tension pour le tube (Iw) et de la composante déphasée de 90° pour le ballast (Ib).
U = 220 volts ; I = 0,3 ampère ; sin φ 60º
- Q = 200 x 0,3 x 60 = 57 VAR
De manière similaire, l'énergie réactive est calculée en multipliant la puissance réactive par le temps. Par conséquent, en fonctionnement pendant 4 heures, la lampe entraînera :
Energie réactive = Q x T = 57 VAR x 4 h = 228 VARh
Lorsqu'un condensateur est ajouté en parallèle sur le système et dimensionné pour tirer un courant précisément égal à celui du ballast, alors :
Le courant capacitif et le courant inductif sont en phase opposée (le courant capacitif est en avance de 90° tandis que le courant inductif est en retard de 90° par rapport à la tension) - ce qui entraîne une annulation de leur somme.
Le courant total équivaut au courant résistif dans le tube, ce qui représente 0,15 ampère.
Avant l'ajout du condensateur :
- Courant total : 0,3 ampère
- Puissance active : U x I x cos phi = 220 x 0,3 x cos 60° = 33 watts
- Puissance réactive : U x I x sin phi = 220 x 0,3 x sin 60° = 57 VARs.
Après l'ajout du condensateur :
- Courant total : 0,15 ampère
- Puissance active : U x I x cos phi = 220 x 0,15 x cos 0° = 33 watts
- Puissance réactive inductive : U x Ib x sin phi = 220 x 0,26 x sin (-90°) = -57 VARs
- Puissance réactive capacitive : U x Ic x sin phi = 220 x 0,26 x sin 90° = 57 VARs
- Puissance réactive totale : U x I x sin phi = 220 x 0,15 x sin 0° = 0 VARs
Autre méthode de calcul de la puissance réactive
En utilisant le théorème de Pythagore, la relation entre les trois puissances est la suivante :
S=√(P²+Q²)
Où :
- S = puissance apparente en voltampère (VA)
- P = puissance active en watt (W)
- Q = puissance réactive en voltampère réactif (VAR)
En utilisant la trigonométrie, les relations pour les puissances entre ϕ, P, Q et S sont les suivantes :
- cos φ = P / S
- tan φ = Q /P
Exemple de la deuxième formule de calcul de la puissance réactive
Par exemple, si pour une période de 10 minutes la puissance active est de 4 W et la puissance réactive de 3 VAR :
- La puissance apparente est de 5 VA,
- Le cos φ est égal à 0,7,
- La tan φ est égale à 0,93.
Lorsque le cos φ se rapproche de 1, la puissance réactive diminue.
En revanche, lorsque la tan φ se rapproche de 1, la puissance réactive augmente.
Qui consomme une puissance réactive ?
Les principaux utilisateurs d'énergie réactive sont les grands consommateurs, en particulier dans l'industrie, qui utilisent des gros équipements énergivores tels que des machines de soudage, des fours à induction et à arc, des moteurs asynchrones, des transformateurs et des lampes fluorescentes. Ces équipements nécessitent un champ magnétique pour fonctionner.
De plus, au fil du temps, l'usure de certaines machines industrielles peut entraîner une augmentation significative de la puissance réactive.
Les consommateurs résidentiels, quant à eux, ont une consommation d'énergie réactive trop faible pour avoir un impact notable sur le réseau.
Quelles conséquences la puissance réactive peut-elle entraîner ?
Les utilisateurs connectés en haute tension (HT), en HTB (C1, C2, C3) et en basse tension au-delà de 36 kVA (C4) seront facturés pour l'énergie réactive en cas de dépassement du seuil établi par les distributeurs. Le calcul du rapport de la tangente phi correspond à l'énergie réactive divisée par l'énergie active. Si ce ratio dépasse 40% (0.4), (la valeur optimale étant 0), le gestionnaire du réseau de distribution (GRD) facturera l'excédent.
Ainsi, le consommateur devra payer des pénalités de novembre à mars et de 6h à 22h, uniquement pour la partie excédant ce seuil de 0.4. Les modalités de calcul de la pénalité sont définies dans le tarif d'utilisation des réseaux publics d'électricité (TURPE). Des solutions de compensation peuvent être mises en place. En dessous de 40% (0.4), les consommateurs ne seront pas facturés.
Une puissance réactive excessive surcharge les réseaux et les transformateurs. Les pénalités encourues incitent ainsi les sites concernés à compenser leurs installations afin de réduire leur puissance réactive et éviter les surcharges des réseaux et des transformateurs.
Pour illustrer en reprenant l'analogie du verre de bière
La puissance active (la bière) combinée à la puissance réactive (la mousse) donne la puissance totale (la quantité totale présente dans le verre) qui circule dans l'installation. En cas de quantité totale excessive dans le verre, il faudra prendre un verre plus grand pour éviter les débordements.
De même, en présence d'une puissance réactive élevée, une capacité plus importante de connexion au réseau électrique, plus de puissance du transformateur et une installation plus conséquente seront nécessaires. La puissance réactive augmente la puissance apparente et, par conséquent, la capacité requise de l'installation.
Comment baisser sa puissance réactive ?
Pour équilibrer l'énergie réactive, il est possible de recourir à des dispositifs adaptés visant à réduire la quantité totale d'énergie prélevée sur le réseau. Il est essentiel d'évaluer le coût d'installation d'un système de compensation par rapport aux économies réalisées. Ainsi, la solution de compensation permettra de diminuer la puissance réactive qui entraînait des pénalités, et ainsi de réduire la facture d'électricité.
La puissance réactive inductive peut être annulée en utilisant des batteries de condensateurs qui apportent de l'énergie réactive aux bobines. En d'autres termes, l'utilisation de batteries de condensateurs permet de compenser, en tout ou en partie, la puissance réactive inductive sans recourir au réseau électrique.
En résumé, la puissance réactive peut entraîner des coûts énergétiques additionnels, surtout pour les gros consommateurs tels que les industries. Ainsi, il est essentiel de bien comprendre sa consommation en puissance réactive et les éventuelles pénalités qui en découlent afin d'évaluer la pertinence de la mise en place d'un système de compensation.
Questions fréquentes sur la puissance réactive
Quelle est la différence entre la puissance active et réactive ?
La puissance active est mesurée en Watt (W) et correspond à l'énergie convertie en chaleur ou en mouvement. Elle représente la partie de l'électricité considérée comme étant "utile".
Quelle est la différence entre la puissance apparente et réactive ?
La puissance apparente est évaluée en Volt Ampère (VA) et représente la combinaison vectorielle de la puissance active et de la puissance réactive.